




















Un sistema de numeración es un conjunto de símbolos y reglas de generación que permiten construir todos los números válidos.
Un sistema de numeración es un conjunto de símbolos y reglas que permiten representar datos numéricos. Los sistemas de numeración actuales son sistemas posicionales, que se caracterizan porque un símbolo tiene distinto valor según la posición que ocupa en la cifra.
Un sistema de numeración puede representarse como
donde:
 es el sistema de numeración considerado (p.ej. decimal, binario, etc.).
es el sistema de numeración considerado (p.ej. decimal, binario, etc.).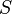 es el conjunto de símbolos permitidos en el sistema. En el caso del sistema decimal son {0,1,...9}; en el binario son {0,1}; en el octal son {0,1,...7}; en el hexadecimal son {0,1,...9,A,B,C,D,E,F}.
es el conjunto de símbolos permitidos en el sistema. En el caso del sistema decimal son {0,1,...9}; en el binario son {0,1}; en el octal son {0,1,...7}; en el hexadecimal son {0,1,...9,A,B,C,D,E,F}. son las reglas que nos indican qué números son válidos en el sistema, y cuáles no. En un sistema de numeración posicional las reglas son bastante simples, mientras que la numeración romana requiere reglas algo más elaboradas.
son las reglas que nos indican qué números son válidos en el sistema, y cuáles no. En un sistema de numeración posicional las reglas son bastante simples, mientras que la numeración romana requiere reglas algo más elaboradas.
NÚMERO DECIMAL 26 TRANSFORMADO AL SISTEMA BINARIO

NÚMERO DECIMAL 8 TRANSFORMADO AL SISTEMA BINARIO

Estas reglas son diferentes para cada sistema de numeración considerado, pero una regla común a todos es que para construir números válidos en un sistema de numeración determinado sólo se pueden utilizar los símbolos permitidos en ese sistema.
Para indicar en qué sistema de numeración se representa una cantidad se añade como subíndice a la derecha el número de símbolos que se pueden representar en dicho sistema.
Ejemplos
- el número 135(10) es un número válido en el sistema decimal que utiliza los símbolos (0, 1, 2, 3, 4, 5, 6, 7, 8, 9), pero el número 12A(10) no lo es, ya que utiliza un símbolo A no válido en este sistema decimal.
- el número 35(8) es un número válido en el sistema octal que utiliza los símbolos (0, 1, 2, 3, 4, 5, 6, 7) , pero el número 39(8) no lo es, ya que el símbolo 9 no es un símbolo válido en este sistema octal.
- el número F1E4(16) es un número válido en el sistema hexadecimal que utiliza los símbolos (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F), pero el número FKE4(16) no lo es, ya que el símbolo K no es un símbolo válido en este sistema hexadecimal.
- Las lenguas naturales sin ser sistemas formales son sistemas que generalmente cuentan con un procedimiento para nombrar los numerales. La base de los sistemas encontrados en las lenguas del mundo son la base 10 y la base 20, ya que dichos sistemas se originaron en el contaje de dedos de manos (y a veces también pies)
binario:
Clasificación
Los sistemas de numeración pueden clasificarse en dos grandes grupos: posicionales y no-posicionales:
- En los sistemas no-posicionales los dígitos tienen el valor del símbolo utilizado, que no depende de la posición (columna) que ocupan en el número.
- En los sistemas de numeración ponderados o posicionales el valor de un dígito depende tanto del símbolo utilizado, como de la posición que ése símbolo ocupa en el número.
En los sistemas no-posicionales los dígitos tienen el valor del símbolo utilizado, que no depende de la posición (columna) que ocupan en el número.
En los sistemas de numeración ponderados o posicionales el valor de un dígito depende tanto del símbolo utilizado, como de la posición que ése símbolo ocupa en el número.
Por ejemplo, el sistema de numeración egipcio es no posicional, en cambio el babilónico es posicional. Las lenguas naturales poseen sistemas de numeración posicionales basados en base 10 ó 20, a veces con subsistemas de cinco elementos. Además, en algunas pocas lenguas los numerales básicos a partir de cuatro tienen nombres basados en numerales más pequeños.
Sistemas de numeración no posicionales
Estos son los más primitivos se usaban por ejemplo los dedos de la mano para representar la cantidad cinco y después se hablaba de cuántas manos se tenía. También se sabe que se usaba cuerdas con nudos para representar cantidad. Tiene mucho que ver con la coordinabilidad entre conjuntos. Entre ellos están los sistemas del antiguo Egipto, el sistema de numeración romana, y los usados en Mesoamérica por mayas, aztecas y otros pueblos .
Sistemas de numeración semi posicionales
El sistema de los números romanos no es estrictamente posicional. Por esto, es muy complejo diseñar algoritmos de uso general (por ejemplo, para sumar, restar, multiplicar o dividir). Como ejemplo, en el número romano XCIX (99 decimal) los numerales X (10 decimal) del inicio y del fin de la cifra equivalen siempre al mismo valor, sin importar su posición dentro de la cifra.
Sistemas de numeración posicionales
El número de símbolos permitidos en un sistema de numeración posicional se conoce como base del sistema de numeración. Si un sistema de numeración posicional tiene base b significa que disponemos de b símbolos diferentes para escribir los números, y que b unidades forman una unidad de orden superior.
- Ejemplo en el sistema de numeración decimal
Si contamos desde 0, incrementando una unidad cada vez, al llegar a 9 unidades, hemos agotado los símbolos disponibles, y si queremos seguir contando no disponemos de un nuevo símbolo para representar la cantidad que hemos contado. Por tanto añadimos una nueva columna a la izquierda del número, reutilizamos los símbolos de que disponemos, decimos que tenemos una unidad de segundo orden (decena), ponemos a cero las unidades, y seguimos contando.
De igual forma, cuando contamos hasta 99, hemos agotado los símbolos disponibles para las dos columnas; por tanto si contamos (sumamos) una unidad más, debemos poner a cero la columna de la derecha y sumar 1 a la de la izquierda (decenas). Pero la columna de la izquierda ya ha agotado los símbolos disponibles, así que la ponemos a cero, y sumamos 1 a la siguiente columna (centena). Como resultado nos queda que 99+1=100.
El cuentakilómetros mecánico, al utilizar el sistema de numeración posicional decimal, nos muestra lo anterior: va sumando 1 a la columna de la derecha y cuando la rueda de esa columna ha completado una vuelta (se agotan los símbolos), se pone a cero y se añade una unidad a la siguiente columna de la izquierda.
Pero estamos tan habituados a contar usando el sistema decimal que no somos conscientes de este comportamiento, y damos por hecho que 99+1=100, sin pararnos a pensar en el significado que encierra esa expresión.
Tal es la costumbre de calcular en decimal que la mayoría de la población ni siquiera se imagina que puedan existir otros sistemas de numeración diferentes al de base 10, y tan válidos y útiles como este. Entre esos sistemas se encuentran el de base 2 sistema binario, de base 8 sistema octal y el de base 16 sistema hexadecimal. También los antiguos mayas tuvieron un sistema de numeración posicional el cual ya no se usa.
Teorema Fundamental de la numeración
Este teorema establece la forma general de construir números en un sistema de numeración posicional. Primero estableceremos unas definiciones básicas:
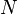 , número válido en el sistema de numeración.
, número válido en el sistema de numeración. , base del sistema de numeración. Número de símbolos permitidos en el sistema.
, base del sistema de numeración. Número de símbolos permitidos en el sistema. , un símbolo cualquiera de los permitidos en el sistema de numeración.
, un símbolo cualquiera de los permitidos en el sistema de numeración. ,: número de dígitos de la parte entera.
,: número de dígitos de la parte entera. , coma fraccionaria. Símbolo utilizado para separar la parte entera de un número de su parte fraccionaria.
, coma fraccionaria. Símbolo utilizado para separar la parte entera de un número de su parte fraccionaria. ,: número de dígitos de la parte decimal.
,: número de dígitos de la parte decimal.
La fórmula general para construir un número N, con un número finito de decimales, en un sistema de numeración posicional de base b es la siguiente:
El valor total del número será la suma de cada dígito multiplicado por la potencia de la base correspondiente a la posición que ocupa en el número.
Esta representación posibilita la realización de sencillos algoritmos para la ejecución de operaciones aritméticas.
Ejemplo en el sistema decimal
En el sistema decimal los símbolos válidos para construir números son {0,1,...9} (0 hasta 9, ambos incluidos), por tanto la base (el número de símbolos válidos en el sistema) es diez
En la figura inferior podemos ver el teorema fundamental de la numeración aplicado al sistema decimal.


Los dígitos a la izquierda de la coma fraccionaria representados por dn ... d2 d1 d0 , toman el valor correspondiente a las potencias positivas de la base (10 en el sistema decimal), en función de la posición que ocupan en el número, y representan respectivamente al dígito de las n-unidades (10n), centenas (10²=100), decenas (10¹=10) y unidades (100=1), ya que como se ve en el gráfico están colocados en las posiciones n..., tercera, segunda y primera a la izquierda de la coma fraccionaria.
Los dígitos a la derecha de la coma fraccionaria d-1, d-2, d-3 ... d-n representan respectivamente al dígito de las décimas (10-1=0,1), centésimas (10-2=0,01), milésimas (10-3=0,001) y n-ésimas (10-n) .
Por ejemplo, el número 1492,36 en decimal, puede expresarse como: 1492/36

Ejemplo en el sistema binario
Tomemos ahora el sistema binario o de base 2. En este sistema los dígitos válidos son {0,1}, y dos unidades forman una unidad de orden superior.
En la figura inferior podemos ver el teorema fundamental de la numeración aplicado al sistema binario.


Seguimos con el ejemplo del cuentakilómetros visto arriba. En este caso las ruedas no tienen 10 símbolos (0 al 9) como en el caso del sistema decimal. En el sistema binario la base es 2, lo que quiere decir que sólo disponemos de 2 símbolos {0,1} para construir todos los números binarios.
En el sistema binario, para representar cifras mayores que 1 se combinan los 2 símbolos {0,1} y agrega una segunda columna de un orden superior.
Aquí las ruedas del cuentakilómetros dan una vuelta cada dos unidades. Por tanto, una vez que contamos (sumamos) dos hemos agotado los símbolos disponibles para esa columna, y debemos poner a cero la columna y usar otra columna a la izquierda.
Así, si contamos en binario, tras el número 0(2 viene el 1(2, pero si contamos una unidad más debemos usar otra columna, resultando 10(2
Sigamos contando 0(2,1(2,10(2,11(2. Al añadir una unidad a la columna de las unidades, esa columna ha dado la vuelta (ha agotado los símbolos disponibles), y debemos formar una unidad de segundo orden, pero como ya hay una, también agotaremos los símbolos disponibles para esa columna, y debemos formar una unidad de tercer orden o 100(2. Así, en el sistema binario 11(2 + 1(2 + 100(2
Ejemplos:
- El número
 está formado por un solo símbolo repetido tres veces. No obstante, cada uno de esos símbolos tiene un valor diferente, que depende de la posición que ocupa en el número. Así, el primer 1 (empezando por la izquierda) representa un valor de
está formado por un solo símbolo repetido tres veces. No obstante, cada uno de esos símbolos tiene un valor diferente, que depende de la posición que ocupa en el número. Así, el primer 1 (empezando por la izquierda) representa un valor de  , el segundo de
, el segundo de  y el tercero de
y el tercero de  , dando como resultado el valor del número:
, dando como resultado el valor del número:  .
.
ENLACES





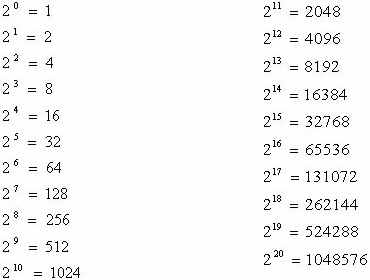






No hay comentarios:
Publicar un comentario